IBDP Maths AI Resources

CONCEPT

Formulas

use of calc

Practices

Concepts

Complex Numbers (HL Only)

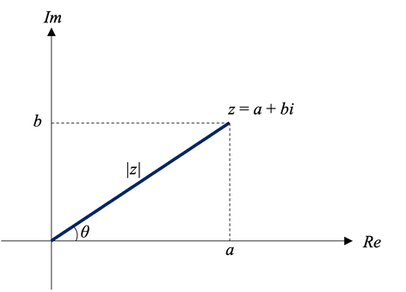
it is written in the format: z = a + bi

a is the real part, (Re(z))
b is the imaginary part, (Im(z))
i is the imaginary unit, i ² = – 1

(is a useless thing so people can solve something that is "unsolvable" originally)

Operations

Addition:

Subtraction:

Multiplication:

Division:

Argand Diagram (on the complex plane)

The x-axis is the real axis

The y-axis is the imaginary axis

Polar Form

z = r (cos θ + i sin θ)

where

Euler's formula

the exponential form is

De Moivre's Theorem

the n-th root of a complex number is given by:

where the roots are equally spaced around the complex plane.

Up

Matrices and Determinants (HL Only)

A matrix is a rectangular array of numbers arranged in rows and columns. Matrices are used to solve systems of equations, transformations, and various applications in physics, engineering, and economics.

A general m × n matrix is written as:

m is the number of rows
n is the number of columns
m = n, the matrix is square

Operations

Addition:

Subtraction:

Scalar Multiplication:

Matrix Multiplication:

And matrix multiplication is not commutative: AB ≠ BA

Identity Matrix:

Transpose of Matrix:

Determinants (HL)

The determinant of a square matrix is a scalar value that provides important information about the matrix, such as whether it is invertible.

For a 2 × 2 matrix:

The 2 × 2 determinant:

For a 3 × 3 matrix:

The 3 × 3 determinant:

Inverse of a matrix (HL)

A square matrix A is invertible if and only if its determinant is nonzero det⁡(A) ≠ 0. The inverse satisfies:

The 2 × 2 inverse of a matrix:

Matrix transformations (HL)

the exponential form is

Up

Formulas

1 / Item Title